TAG:突破
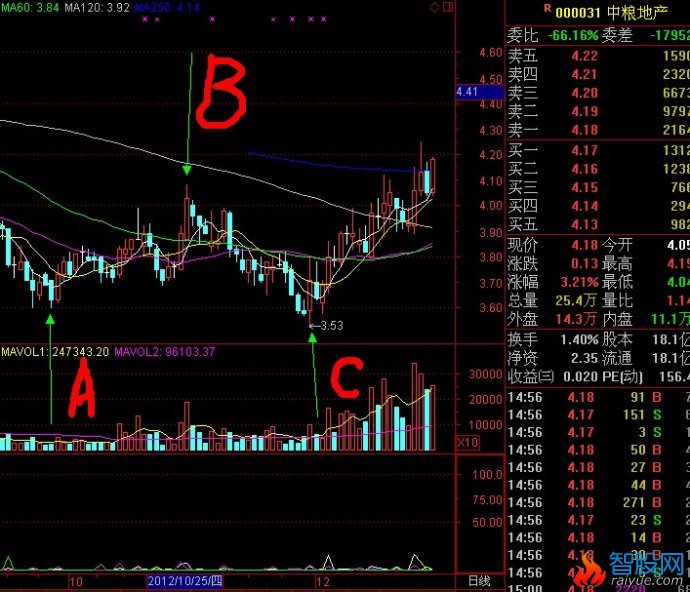
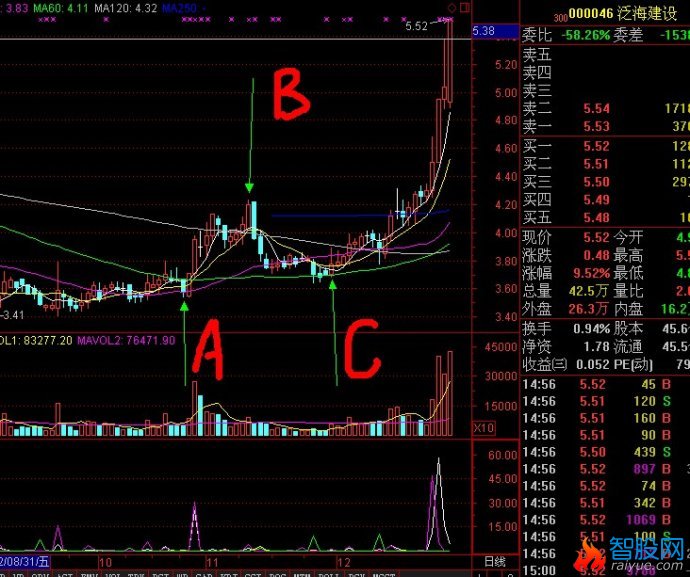

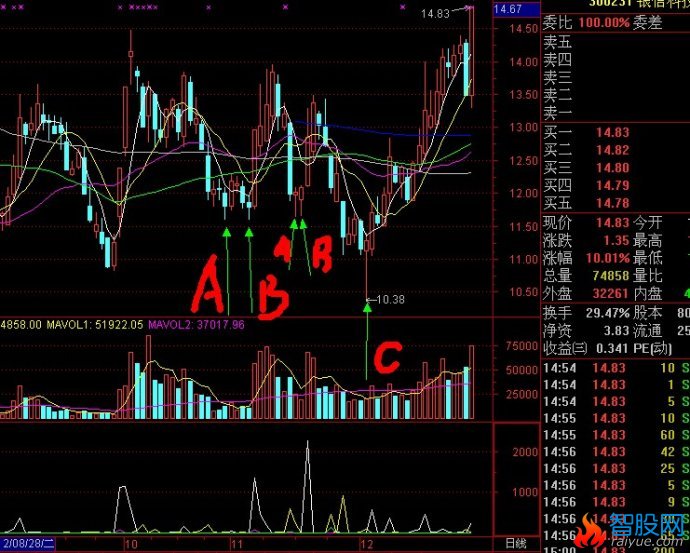
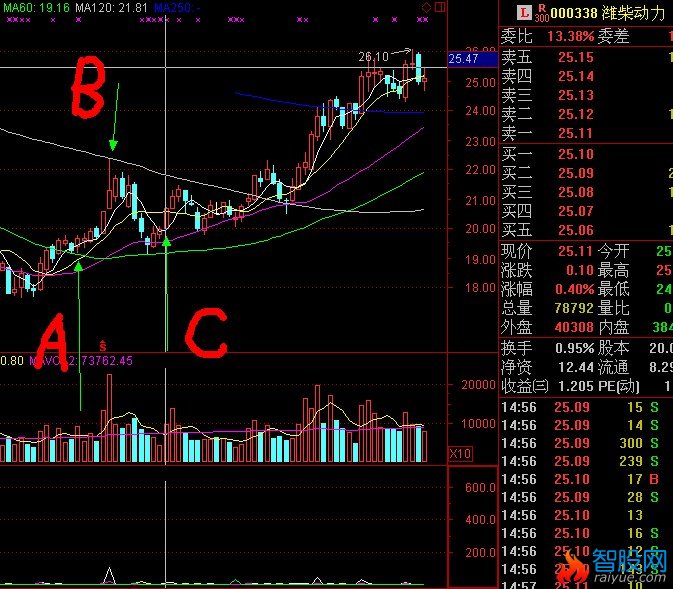

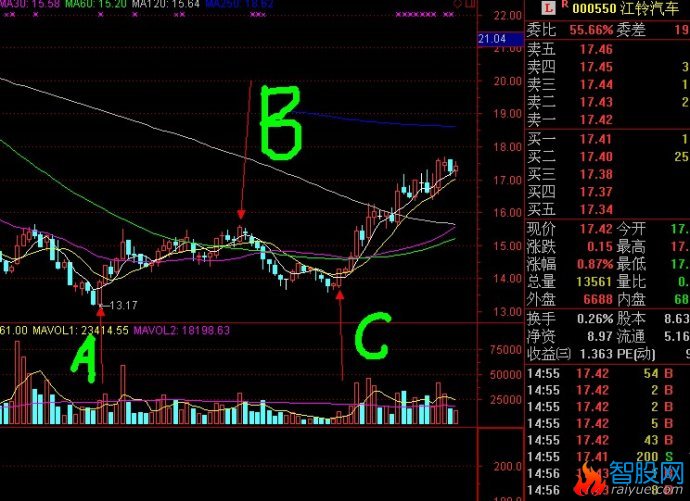
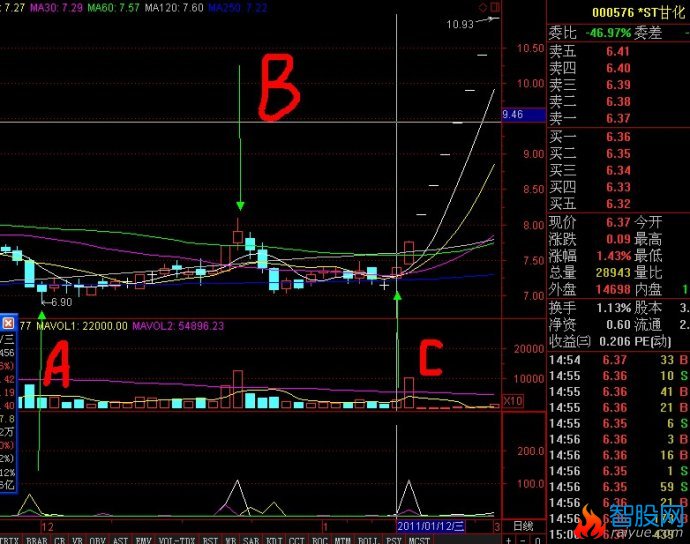
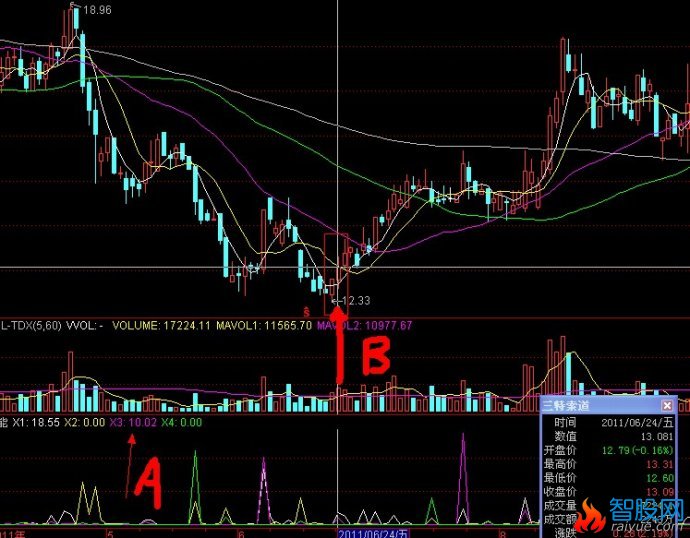
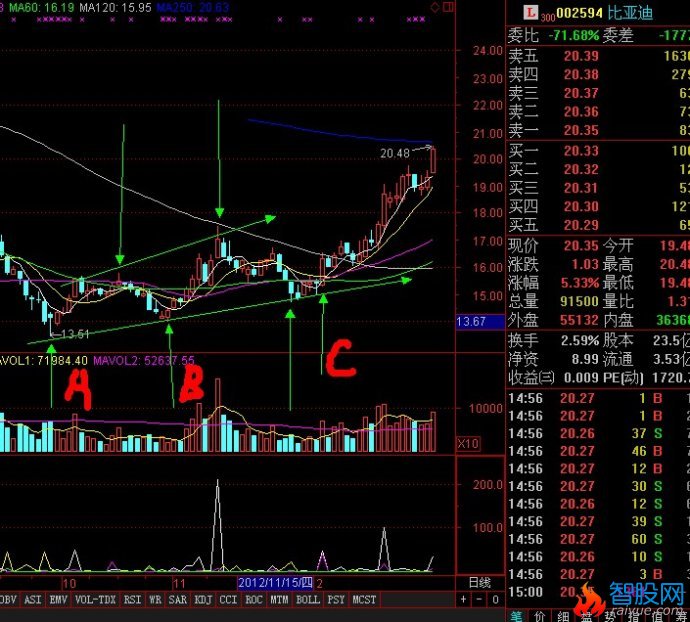
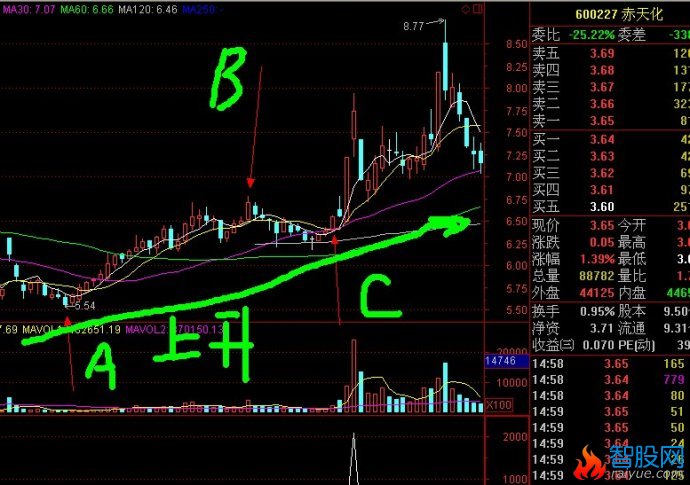
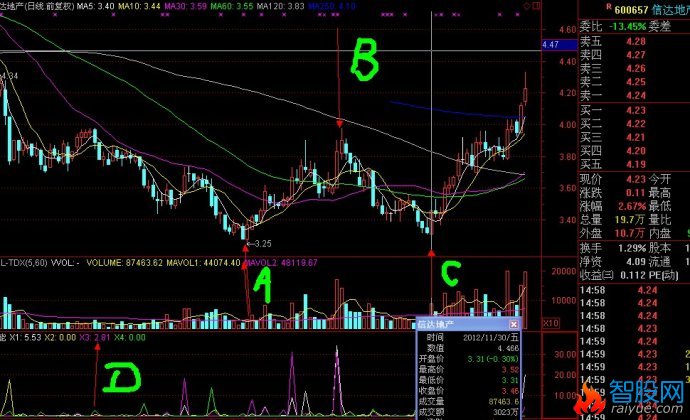
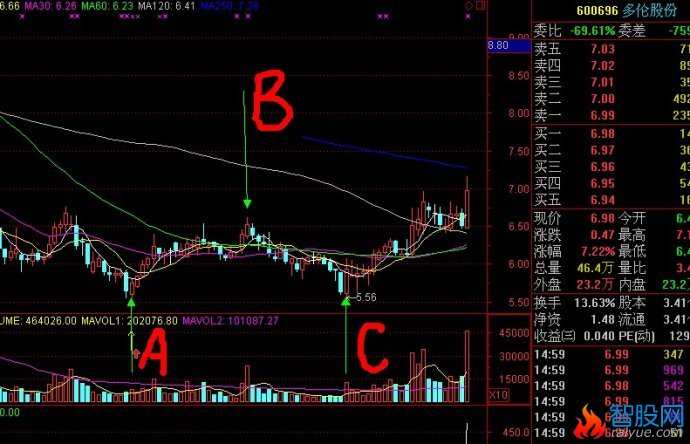
二次探底买入临界点的确立方法和经典案例
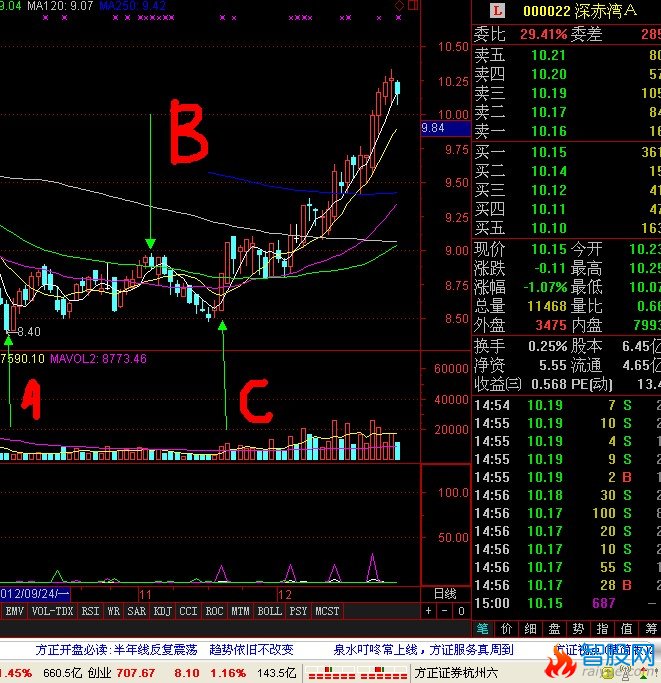
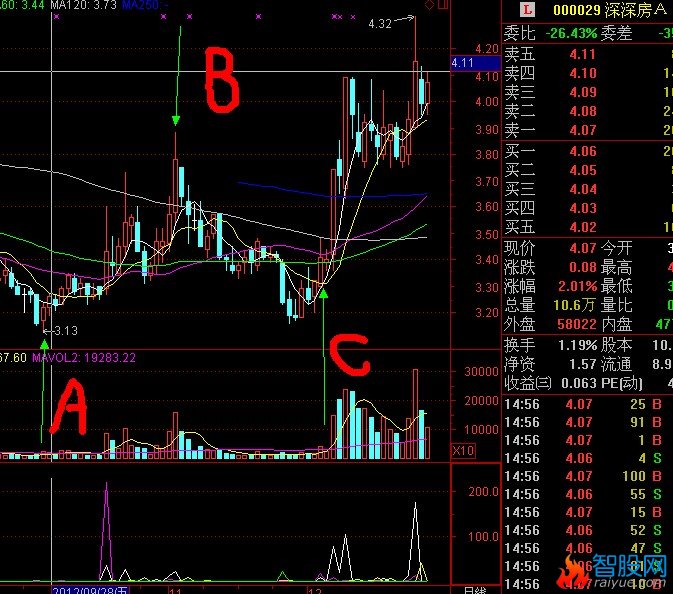
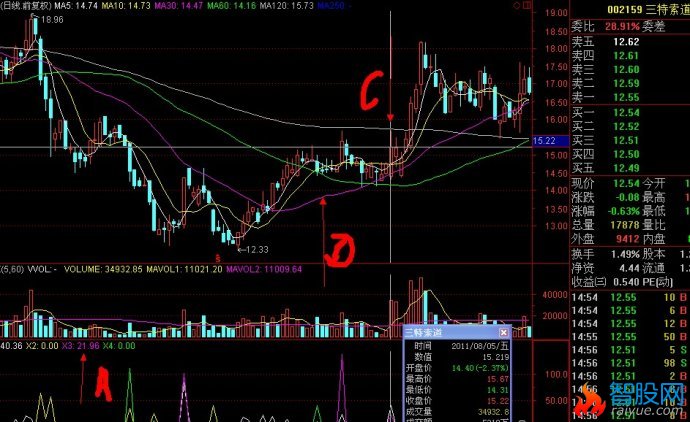
如图中的C线为临界启动买入点,以下有详细的原理解释
两个定理:
1):股价在二次探底过程中的底部区域,如果某日的上涨动能大于以前三天最大动能的1.2倍以上,那么股价上攻的概率较大(当日为买入临界点)。
2): 股价在二次探顶过程中的顶部区域,如果某日的下降动能大于以前三天最大动能的1.2倍以上,那么股价下降的概率较大(当日为卖出临界点)。
根据定理1),图中C线为上攻启动临界点。
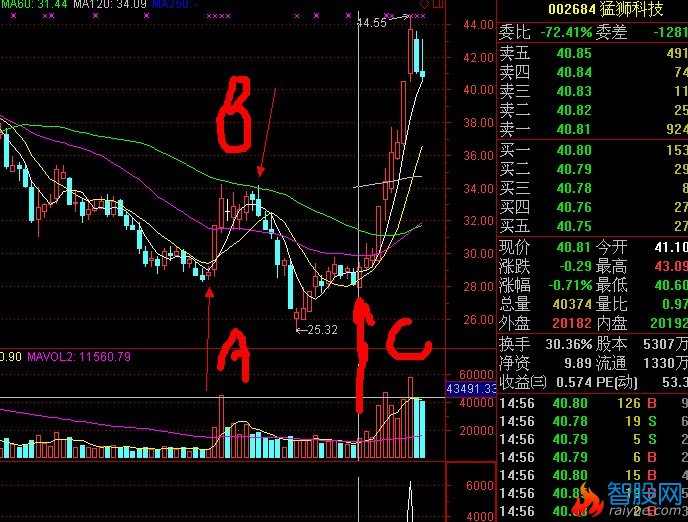
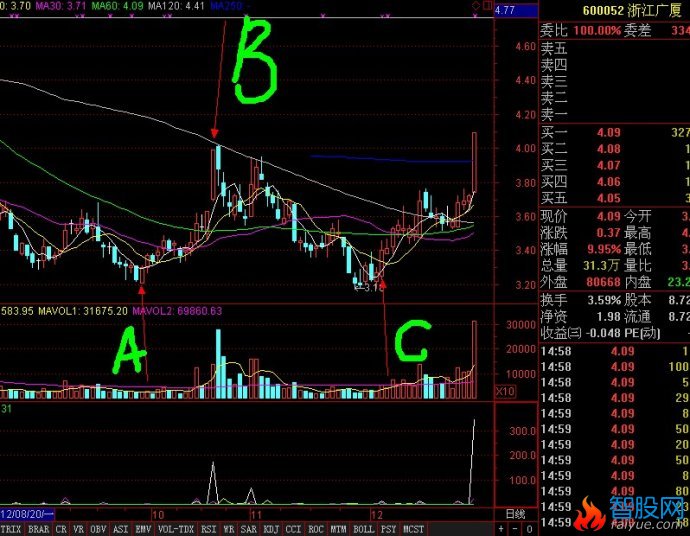
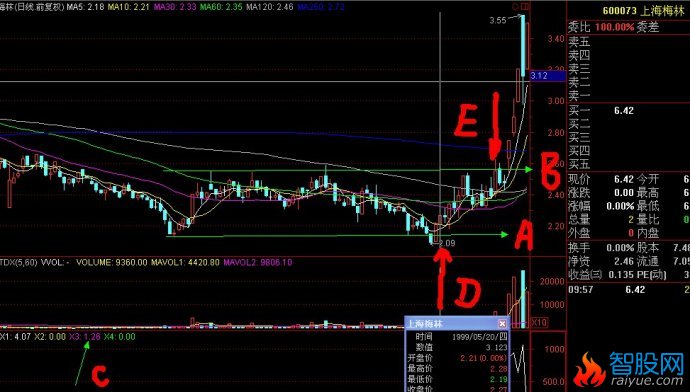
如图,A,B,,C,三条线。股价从A线的最低价反弹到B线后二次探底到C线。在这个过程中,A到B的过程应该是放量上涨。B到C的过程是缩量回调,并且回调收盘价不能跌破A线的最低点。如果满足以上条件,那么可以将C线附近的区域定义为股价的底部。(C线为买入临界点)
现在就引出了一个问题,股价在底部启动上攻的日子怎样确立呢?
学习物理专业的博友可能知道《狭义相对论》,这本书基于两个公理:一是光速不变原理,二是所有参照系都是等价的。根据这两个公里推导出著名的质能方程E=MC*C。人们再根据这个方程制造出了原子弹,而原子弹的成功爆炸又证明了相对论的正确性。
我是学习物理的,就时常时常想,股市中有没有不经过证明就存在的命题呢?我提出了一下的两个命题。
第一,人性不变原理。
第二,所有相同价位作为参考都是等效的。
那么根据这两个命题我们能够得到股市中的什么结论呢?我首根据股市的基础知识自定义了两个概念。
1,买方量价能,简称买压或者上涨功能,用CCB表示。当日成交量(均价)乘以当日上涨的幅度叫买压。公式为
GG:=AMOUNT/VOL;
M1:=((GG-REF(GG,1))/REF(GG,1))*((GG-REF(GG,1))/REF(GG,1))*10000;
M2:=((REF(GG,1)-GG)/GG)*((REF(GG,1)-GG)/GG)*10000;
CCB:=SUM(IF(GG>REF(GG,1),(10000*VOL/FINANCE(7))*M1,0),1);
CCS:=SUM(IF(GG
2,卖方量价能,简称卖压或者下降动能,用CCS表示。当日成交量(均价)乘以当日下降的幅度叫卖压。公式为
CCS:=SUM(IF(GG
有了这两个定义,就能够把定性的描述转化为定量的描述,即用公式表达出来
,例如,放量上涨,缩量回调的两根K线多数时候有CCB>CCS。而放量杀跌,缩量反抽时候有CCB。股市要上涨,必须有买压大于卖压。而买压大于卖压,股市不一定上涨,卖压大于买压,股市一定下跌。这一点博友们必须注意,切记!切记!。
现在我把股市相对论的基本结论描述如下:
任何两个相同价位的点位期间积累的买压大于卖压,那么股市上涨的概率较大。任何两个相同价位的点位期间积累的卖压大于买压,那么股市下降的概率极大。
表达式:sum(ccb,n)>sum(ccs,n)有股价上涨的较大概率。
sum(ccb,n)有股价下降的较大概率。
提出两个定理:
1):股价在二次探底过程中的底部区域,如果某日的上涨动能大于以前三天最大动能的1.2倍以上,那么股价上攻的概率较大(当日为买入临界点)。
2): 股价在二次探顶过程中的顶部区域,如果某日的下降动能大于以前三天最大动能的1.2倍以上,那么股价下降的概率较大(当日为卖出临界点)。
根据定理1),图中C线为上攻启动临界点。
该形态的选股公式
GG:=AMOUNT/VOL;
M1:=((GG-REF(GG,1))/REF(GG,1))*((GG-REF(GG,1))/REF(GG,1))*10000;
M2:=((REF(GG,1)-GG)/GG)*((REF(GG,1)-GG)/GG)*10000;
CCB:=SUM(IF(GG>REF(GG,1),(10000*VOL/FINANCE(7))*M1,0),1);
CCS:=SUM(IF(GG
B1:=(CCB+CCS);
B2:=MAX(REF(B1,1),REF(B1,2));
B0:=MAX(B2,REF(B1,3));
B3:=MAX(B0,REF(B1,4));
B4:=MAX(B3,REF(B1,5));
B5:=MAX(B4,REF(B1,6));
B6:=MAX(B5,REF(B1,7));
B7:=MAX(B6,REF(B1,8));
B8:=MAX(B7,REF(B1,9));
B9:=MAX(B8,REF(B1,10));
B10:=MAX(B9,REF(B1,11));
B11:=MAX(B10,REF(B1,12));
B12:=MAX(B11,REF(B1,13));
B13:=MAX(B12,REF(B1,14));
B14:=MAX(B13,REF(B1,15));
B15:=MAX(B14,REF(B1,16));
B16:=MAX(B15,REF(B1,17));
B:=CCB>1.2*B0&&REF(CCB,1)
REF(CCB,3)